Question

Prove: If n is a positiveinteger and n2 is
divisible by 3, then n is divisible by3.

Answer 1

If
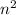`n^2` is divisible by 3, the n is also divisible by 3.

Explanation:

We will prove this with the help of contrapositive that is we prove that if n is not divisible by 3, then,
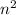`n^2` is not divisible by 3.

Let n not be divisible by 3. Then
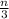`(n)/(3)` can be written in the form of fraction
`(x)/(y)`, where x and y are co-prime to each other or in other words the fraction is in lowest form.

Now, squaring

`(n^2)/(9) = (x^2)/(y^2)`

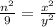
Thus,

`n^2 = (9x^2)/(y^2)`

`(n^2)/(3) = (3x^2)/(y^2)`

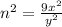
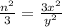
It can be clearly seen that the fraction
`(3x^2)/(y^2)` is in lowest form.

Hence,
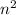`n^2` is not divisible by 3.

Thus, by contrapositivity if
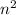`n^2` is divisible by 3, the n is also divisible by 3.