Question

Applicants for temporary office work at Carter Temporary Help Agency who have successfully completed an administrative assistant course are then placed in suitable positions by Nancy Dwyer and Darla Newberg. Employers who hire temporary help through the agency return a card indicating satisfaction or dissatisfaction with the work performance of those hired. From past experience it is known that 80% of the employees placed by Nancy are rated as satisfactory, and 65% of those placed by Darla are rated as satisfactory. Darla places 55% of the temporary office help at the agency, and Nancy places the remaining 45%. If a Carter office worker is rated unsatisfactory, what is the probability that he or she was placed by Darla? (Round your answer to three decimal places.)

Answer 1

0.681

Explanation:

Let's define the following events:

S: a Carter office worker is rated satisfactory

U : a Carter office worker is rated unsatisfactory

ND: a Carter office worker is placed by Nancy Dwyer

DN: a Carter office worker is placed by Darla Newberg

We have from the original text that

P(S | ND) = 0.8, this implies that P(U | ND) = 0.2.

P(S | DN) = 0.65, this implies that P(U | DN) = 0.35. Besides

P(DN) = 0.55 and P(ND) = 0.45, then we are looking for

P(DN | U), using the Bayes' formula we have

P(DN | U) =
`(P(U | DN)P(DN))/(P(U | DN)P(DN) + P(U | ND)P(ND))` =
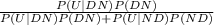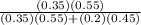`((0.35)(0.55))/((0.35)(0.55)+(0.2)(0.45))`=0.681