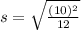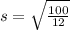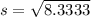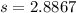Question

A random variable x is uniformly distributed over the interval (-4, 6). Find the standard deviation of x. (Note: Uniform distribution is a distribution where the PDF value is the same across all x values)

Answer 1

The standard deviation of x is 2.8867

Explanation:

The standard deviation of variable x that follows a uniform distribution is calculated as:

`s = \sqrt{((b-a)^(2) )/(12) }`

Where (a,b) is the interval where x is defined.

So, replacing a by -4 and b by 6, the standard deviation is:

`s = \sqrt{((6-(-4))^(2) )/(12) }`

`s = \sqrt{((10)^(2) )/(12) }`

`s=\sqrt{(100)/(12) }`

`s=√(8.3333)`

`s=2.8867`