Question

One side of a triangular lot is 150 ft and the angel oppiste this side is 55 degrees. Another angel is 63 degrees. Determine how much fencing is needed to enclose it.

Answer 1

474.84 ft of fencing is needed

Explanation:

We know that the angles of a triangle sum up 180º. We already know 2 of the triangle's angles (55º and 63º). Therefore the third angle measures:

180 - 55 - 63 = 62.

To know how much fencing is needed, we need the perimeter of the triangle, so we need to find out how much the other sides of the lot measure.

We will use law of sins to solve this problem.

First we solve for y:

`(150)/(sin55)= (y)/(sin63)  \\y=150 (sin63)/(sin55)\\y=133.65/.8191\\y=163.16`

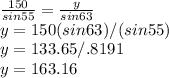
Now we solve for the other side of the lot, x:

`(150)/(sin55)=(x)/(sin62)\\  x=150(sin62)/(sin55)\\x=150(.8829)/.8191\\x=132.435/.8191\\x=161.68`

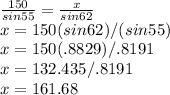
Now that we have the measures of all the sides we sum them up

total fencing needed= 150 + 163.16 + 161.68 = 474.84