Answer:
The age of this sample is 13,417 years.
Explanation:
The amount of carbon 14 present in a sample after t years is given by the following equation:
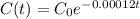
Estimate the age of a sample of wood discoverd by a arecheologist if the carbon level in the sampleis only 20% of it orginal carbon 14 level.
The problem asks us to find the value of t when
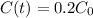
So:
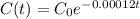
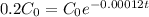
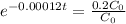
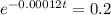
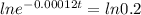
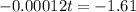
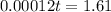
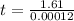
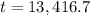
The age of this sample is 13,417 years.