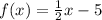Question

PLEASE HELP ASAP PLEASE

Choose the equation below that represents the line passing through the point (2, -4) with a slope of one half.


y = one half x + 5

y = one half x − 3

y = one half x − 5

y = one half x + 3

Answer 1

The equation that represents the line passing through the point (2, -4) with a slope of one half is

`f(x) = (1)/(2)x - 5`

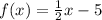
Explanation:

The equation of a line can be described by a first order equation in the following format:

`f(x) = ax + b`

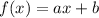
In which a is the slope of the line.

Solution:

The line slope is
`(1)/(2)`, so
`a = (1)/(2)`.

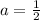The equation of the line now is:

`f(x) = (1)/(2)x + b`

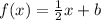
The problem states that the line passes through the point(2,-4). This means that when x = 2, f(x) = -4

So:

`f(x) = (1)/(2)x + b`

`-4 = (1)/(2)*(2) + b`

`-4 = 1 + b`

`b = -5`

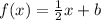
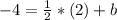
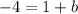
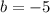
So, the equation that represents the line passing through the point (2, -4) with a slope of one half is

`f(x) = (1)/(2)x - 5`