Question

Let A and B be non-empty, bounded subsets of R. (a) Why does sup(AUB) exist? (b) Prove that sup(AUB) = max{sup A, sup B}.

Answer 1

90% of people marry there 7th grade love. since u have read this, u will be told good news tonight. if u don't pass this on nine comments your worst week starts now this isn't fake. apparently if u copy and paste this on ten comments in the next ten minutes you will have the best day of your life tomorrow. you will either get kissed or asked out in the next 53 minutes someone will say i love you

Explanation:

Answer 2

Answer with Step-by-step explanation:

Let A and B be non- empty bounded subset of R

a.We have to find why
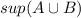`sup(A\cup B)`exist

If A and B are bounded set

Then there exist constant such that

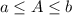`a\leq A\leq b` and
`c\leq B\leq d`

Then , sup of A =b and sup of B=d

When a set is bounded then all elements lie in the set are lie between the constants s and t.

All elements are less than or equal to t then t is supremum of set.

Because both set are bounded and sup of both set A and B are exist.All elements A union B are less than or equal to sup A or sup B.

`sup(A\cup B)=max(sup A, sup B)`

Then,
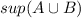`sup (A\cup B)` exist.

b.We have to prove that

`sup (A\cup B)=max(sup A,sup B)`

Suppose ,A =(1,2) and B=(2,3)

Sup A=2 , sup B=3

`(A\cup B)=(1,2)\cup (2,3)`

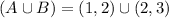
Upper bound of
`A\cup B)=3`

Hence,
`Sup (A\cup B)=3`

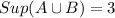
If A=(4,5),B=(2,3)

Sup A=5,Sup B=3

`A\cup B=(4,5)\cup (2,3)`

`Sup(A\cup B)=5`

Hence,
`Sup(A\cup B)=5`

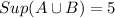
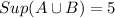
Hence, we can say that
`sup(A\cup B)=max(sup A,sup B)`.