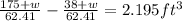Question

How much extra water does a 21.5 ft, 175-lb concrete canoe displace compared to an ultra-lightweight 38-lb Kevlar canoe of the same size carrying the same load?

Answer 1

The volume of the extra water is
`2.195 ft^(3)`

Solution:

As per the question:

Mass of the canoe,
`m_(c) = 175 lb + w`

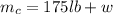
Height of the canoe, h = 21.5 ft

Mass of the kevlar canoe,
`m_(Kc) = 38 lb + w`

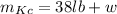
Now, we know that, bouyant force equals the weight of the fluid displaced:

Now,

`V\rho g = mg`

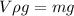
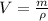`V = (m)/(\rho)` (1)

where

V = volume

`\rho = 62.41 lb/ft^(3)` = density

m = mass

Now, for the canoe,

Using eqn (1):

`V_(c) = (m_(c) + w)/(\rho)`

`V_(c) = (175 + w)/(62.41)`

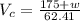
Similarly, for Kevlar canoe:

`V_(Kc) = (38 + w)/(62.41)`

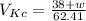
Now, for the excess volume:

V =
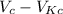
`V_(c) - V_(Kc)`

V =
`(175 + w)/(62.41) - (38 + w)/(62.41) = 2.195 ft^(3)`