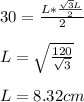Answer: The sides length are 8.32 cm
Explanation:
An equilateral triangle has all his sides of the same lenght, so we assume that the triangle has an L lenght in his sides.
The area of a triangle is
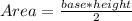 where the base is L, the Area is 30 and an unknown height.
where the base is L, the Area is 30 and an unknown height.
To determine the height, we cut the triangle in half and take one side. By simetry, one side has a base of
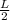 , a hypotenuse of L and a the unknown height.
, a hypotenuse of L and a the unknown height.
Then we apply the Pythagoras theorem, this states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides, or,
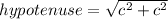 Where one c is
Where one c is
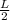 and the other is the height.
and the other is the height.
Then we find one of the c of the equation wich will be the height.
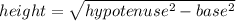
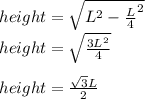
Finally, we use the triangle area mentioned before an find the value of L.