Answer:
a) vertical position at 2s: 50.68 m
b) horizontal position at 2s: 13.05 m
Step-by-step explanation:
This situation is a good example of the projectile motion or parabolic motion, in which the travel of the rock has two components: x-component and y-component. Being the equations to find the position as follows:
x-component:
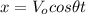 (1)
(1)
Where:
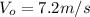 is the rock's initial speed
is the rock's initial speed
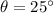 is the angle at which the rock was thrown
is the angle at which the rock was thrown
 is the time
is the time
y-component:
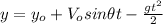 (2)
(2)
Where:
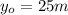 is the initial height of the rock
is the initial height of the rock
 is the height of the rock at 2 s
is the height of the rock at 2 s
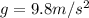 is the acceleration due gravity
is the acceleration due gravity
Knowing this, let's begin with the answers:
a) Vertical position at 2 s:
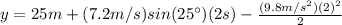 (3)
(3)
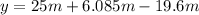 (4)
(4)
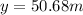 (5) This is the vertical position at 2 s
(5) This is the vertical position at 2 s
b) Horizontal position at 2 s:
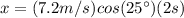 (5)
(5)
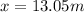 (6) This is the horizontal position at 2 s
(6) This is the horizontal position at 2 s