Answer: The required co-ordinates of Z are (2, 7).
Step-by-step explanation: Given that Y is the midpoint of XZ and the co-ordinates of X are (-10, 9) and the of Y are (-4, 8).
We are to find the co-ordinates of Z.
Let (a, b) represents the co-ordinates of the point Z.
We know that
the co-ordinates of the midpoint of a line segment with endpoints (x, y) and (z, w) are given by
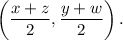
So, according to the given information, we have

and

Thus, the required co-ordinates of Z are (2, 7).