Answer:
You could order 16 different kinds of pizza.
Explanation:
You have those following toppings:
-Pepperoni
-Sausage
-Mushrooms
-Anchovies
The order is not important. For example, if you choose Sausage and Mushrooms toppings, it is the same as Mushrooms and Sausage. So we have a combination problem.
Combination formula:
A formula for the number of possible combinations of r objects from a set of n objects is:
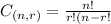
How many different kinds of pizza could you order?
The total T is given by
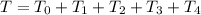
 is the number of pizzas in which there are no toppings. So
is the number of pizzas in which there are no toppings. So
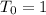
 is the number of pizzas in which there are one topping
is the number of pizzas in which there are one topping
 is a combination of 1 topping from a set of 4 toppings. So:
is a combination of 1 topping from a set of 4 toppings. So:
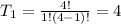
 is the number of pizzas in which there are two toppings
is the number of pizzas in which there are two toppings
 is a combination of 2 toppings from a set of 4 toppings. So:
is a combination of 2 toppings from a set of 4 toppings. So:
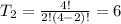
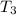 is the number of pizzas in which there are three toppings
is the number of pizzas in which there are three toppings
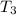 is a combination of 3 toppings from a set of 4 toppings. So:
is a combination of 3 toppings from a set of 4 toppings. So:
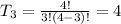
 is the number of pizzas in which there are four toppings. So
is the number of pizzas in which there are four toppings. So
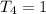
Replacing it in T
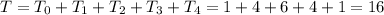
You could order 16 different kinds of pizza.