Question

Of the eighth graders at the Paxson School, 7 played basketball, 9 played volleyball, 10 played soccer, 1 played basketball and volleyball only, 1 played basketball and soccer only, 2 played volleyball and soccer only, and 2 played volleyball, basketball, and soccer. How many played one or more of the three sports?

Answer 1

Answer: There are 18 players who played one or more of the three sports.

Explanation:

Since we have given that

Number of students played basketball = 7

Number of students played volleyball = 9

Number of students played soccer = 10

Number of students played basketball and volleyball = 1

Number of students played volleyball and soccer = 2

Number of students played volleyball, basketball and soccer = 2

Number of students who played basketball only is given by

`7-1-1-2=3`

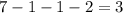
Number of students who played volleyball only is given by

`9-1-2-2\\\\=4`

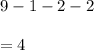
Number of students who played soccer only is given by

`10-1-2-2\\\\=5`

So, Number of students one or more of the three sports is given by

`3+4+5+1+1+2+2\\\\=18`

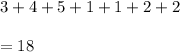
Hence, there are 18 players who played one or more of the three sports.

Answer 2

18

Explanation:

There are

• 7 played basketball;
• 10 played soccer;
• 9 played volleyball;
• 1 played only basketball and volleyball;
• 1 played only basketball and soccer;
• 2 played only volleyball and soccer;
• 2 played basketball, volleyball and soccer.

So,

• 3 played basketball and volleyball;
• 3 played basketball and soccer;
• 4 played volleyball and soccer;
• 7 - 1 - 1 - 2 = 3 played only basketball;
• 10 - 1 - 2 - 2 = 5 played only soccer;
• 9 - 1 - 2 - 2 = 4 played only volleyball.

Hence, 3 + 5 + 4 + 1 + 1 + 2 + 2 = 18 played one or more of the three sports