Question

A 15-gram bullet moving at 1502 m/s plunges into 2.5 kg of paraffin wax. The wax was initially at 31°C. Assuming that all the bullet's energy heats the wax, what is its final temperature (in ºC)? Take the mechanical equivalent of heat to be 4 J/cal and the specific heat of wax to be 0.7 cal/g °C

Answer 1

33.4°C .

Step-by-step explanation:

mass of bullet, m = 15 g = 0.015 kg

velocity of bullet, v = 1502 m/s

mass of wax, M = 2.5 kg

Initial temperature of wax, T1 = 31°C

Let T2 be the final temperature of wax.

Specific heat of wax, c = 0.7 cal/g°C = 0.7 x 1000 x 4 J/kg°C = 2800 J/kg°C

The kinetic energy of the bullet is converted into heat energy which is used to heat the wax.

`(1)/(2)mv^(2)= M * c * \left ( T_(2)-T_(1) \right )`

`0.5* 0.015* 1502 * 1502 = 2.5 * 2800 *\left ( T_(2)-31 \right )`

`2.42 =\left ( T_(2)-31 \right )`

`T_(2)=33.4^(o)C`

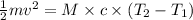
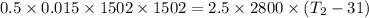
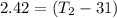
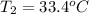
thus, the final temperature of wax is 33.4°C .