Question

If 2x2 + y2 = 17 then evaluate the second derivative of y with respect to x when x = 2 and y = 3. Round your answer to 2 decimal places. Use the hyphen symbol, -, for negative values.

Answer 1

y''=-1.26

Explanation:

We are given that
`2x^2+y^2=17`

We have evaluate the second order derivative of y w.r.t. x when x=2 and y=3.

Differentiate w.r.t x

Then , we get

`4x+2yy'=0`

`2x+yy'=0`

`yy'=-2x`

`y'=-(2x)/(y)`

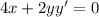
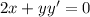
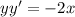
Again differentiate w.r.t.x

Then , we get

`2+(y')^2+yy''=0`
`(u\cdot v)'=u'v+v'u)`

`2+(y')^2+yy''=0`

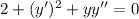
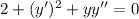
Using value of y'

`yy''=-2-(-(2x)/(y))^2`

`y''=-(2+(-(2x)/(y))^2)/(y)`

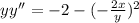
Substitute x=2 and y=3

Then, we get
`y''=-(2+((4)/(3))^2)/(3)`

`y''=-(18+16)/(9* 3)=-(34)/(27)`

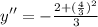
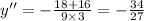
Hence,y''=-1.26