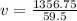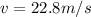Answer:
Part a)
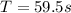
Part b)
v = 22.8 m/s
Step-by-step explanation:
Part a)
Time taken by the taxi to reach the maximum speed is given as
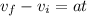
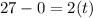
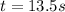
now it moves with constant speed for next 41 s and then finally comes to rest in next 5 s
so total time for which it will move is given as
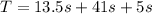
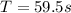
Part b)
Distance covered by the taxi while it accelerate to its maximum speed is given as
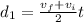
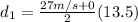
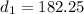
Now it moves for constant speed for next 41 s so distance moved is given as
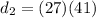
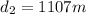
Finally it comes to rest in next 5 s so distance moved in next 5 s

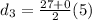
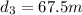
so here we have total distance moved by it is given as
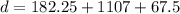
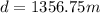
average speed is given as