Question

Write an equation of the line passing through the point (3,2) and is parallel to the line y=\frac{1}{3}x-3

need answer ASAP

Answer 1

Equation of line passing through (3,2) and parallel to line
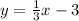`y = (1)/(3)x-3` is:

`y = (1)/(3)x+1`

Explanation:

Given equation of line is:

`y = (1)/(3)x-3`

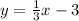
Slope-intercept form of a line is given by:

`y = mx+b`

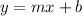
Comparing the given equation of line with general form we get

m = 1/3

Let m1 be the slope of line parallel to given line

Then the equation of line will be:

`y = m_1x+b`

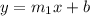
We know, "Slopes of two parallel lines are equal"

Which means

`m_1 = m\\m_1 = (1)/(3)`

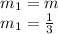
Putting the value of slope

`y = (1)/(3)x+b`

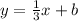
Putting the point (3,2) in the equation

`2 = (1)/(3)(3)+b\\2 = 1+b\\b = 2-1\\b = 1`

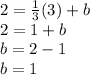
Final equation of line is:

`y = (1)/(3)x+1`

Hence,

Equation of line passing through (3,2) and parallel to line
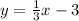`y = (1)/(3)x-3` is:

`y = (1)/(3)x+1`