Answer:
The equation of position and time for a sound wave is
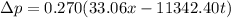 .
.
Step-by-step explanation:
Given that,
Wavelength = 0.190 m
Maximum pressure
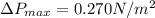
We know that,
The function of position and time for a sound wave,
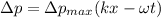 ....(I)
....(I)
We need to calculate the frequency
Using formula of frequency
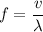
Put the value into the formula
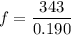
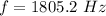
We need to calculate the angular frequency
Using formula of angular frequency
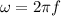
Put the value into the formula
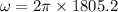
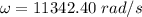
We need to calculate the wave number
Using formula of wave number
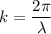
Put the value into the formula
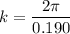
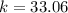
Now, put the value of k and ω in the equation (I)
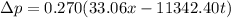
Hence, The equation of position and time for a sound wave is
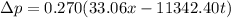 .
.