Question

A researcher conducts a repeated-measures study to evaluate a treatment with a sample of n = 16 participants and obtains a t statistic of t = 1.94. The treatment is expected to increase scores and the sample mean shows an increase. What is the correct decision for a hypothesis test using α = .05?​

Answer 1

Answer with explanation:

Given : Sample size : n= 16

Degree of freedom = n-1=15

The obtained t-statistic value = 1.94

Since, The treatment is expected to increase scores and the sample mean shows an increase.

Let
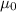`\mu_0` be the population mean before and
`\mu` denotes the population mean after the treatment.

then the related hypothesis will be :-

`\text{Null hypothesis }H_0:\mu_0=\mu\\\\\text{Alternative hypothesis } H_1:\mu_0<\mu`

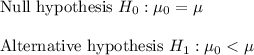
Since the alternative hypothesis is left-tailed, so the test is a left tailed test.

The critical value for
`\alpha=0.05`=1.753

Since, the obtained value (1.94) is greater than the critical value (1.753) so we reject the null hypothesis .

Therefore, we have enough evidence to support the alternative hypothesis.

Hence, we conclude that treatment may successful to increase scores and the sample mean shows an increase.