Question

A Cessna aircraft has a liftoff speed of v = km/h = 33.3 m/s.

a) What minimum constant acceleration does the aircraft require if it is to be airborne after a takeoff run of S = 240 m?
b) How long does it take the aircraft to become airborne?

Answer 1

a) Minimum acceleration is
`a=2.31(m)/(s^(2) )`.

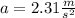b) It will take
`t_(f)=14.41s`.

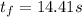Explanation:

Let's order the information.

Initial velocity:
`v_(i)=0m/s`

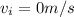
Final velocity:
`v_(f)=33.3m/s`

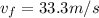
Initial position:
`x_(i)=0m`

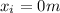
Final position:
`x_(f)=240m`

a) We can use velocity's equation:

`v_(f)^(2) = v_(i)^(2) +2a(x_(f)-x_(i))`

⇒
`a=(v_(f)^(2)-v_(i)^(2))/(2(x_(f)-x_(i)))`

⇒
`a=2.31(m)/(s^(2) )`.

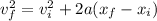
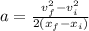
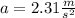b) For this, equation for average acceleration will be helpful. Taking
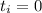`t_(i)=0` and having
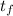`t_(f)` as the unknown time it becomes airborne:

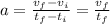
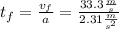
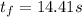`a=(v_(f)-v_(i))/(t_(f)-t_(i)) =(v_(f) )/(t_(f))`

⇒
`t_(f)=(v_(f))/(a)=(33.3(m)/(s))/(2.31(m)/(s^(2)))`

⇒
`t_(f)=14.41s`.