Answer:
Part a)
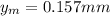
part b)
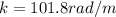
Part c)

Part d)
here since wave is moving in negative direction so the sign of
 must be positive
must be positive
Step-by-step explanation:
As we know that the speed of wave in string is given by

so we have
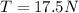
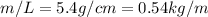
now we have
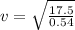
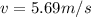
now we have
Part a)
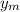 = amplitude of wave
= amplitude of wave
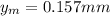
part b)

here we know that
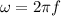
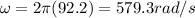
so we have

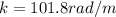
Part c)

Part d)
here since wave is moving in negative direction so the sign of
 must be positive
must be positive