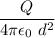Question

A straight wire of length L has a positive charge Q distributed along its length. Find the magnitude of the electric field due to the wire at a point located a distance d from one end of the wire along the line extending from the wire. Imagine that distance d is much greater than the length of the wire. Intuitively, what should the magnitude of the electric field at point P be in this case

Answer 1

Electric Field at a distance d from one end of the wire is
`E=(Q)/(4\pi \epsilon_0(L+d)d)`

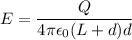
Electric Field when d is much grater than length of the wire =
`(Q)/(4\pi \epsilon_0\ d^2)`

Step-by-step explanation:

Given:

• Total charge over the length of the wire = Q
• Length of the wire = L
• Distance from one end of wire at which electric field is needed to find=d

Let dE be the Electric Field due to the small elemental charge on the wire at a distance x from the one end of the wire and let
`\lambda` be the charge density of the wire

`E=(dq)/(4\pi \epsilon_0x^2)`

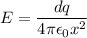
Now integrating it over the entire length varying x from x=d to x=d+L we have and replacing
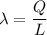`\lambda=(Q)/(L)` we have

`E=\int(\lambda dx)/(4\pi \epsilon_0x^2)\\E=(Q)/(4\pi \epsilon_0 (L+d)(d))`

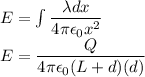
When d is much greater than the length of the wire then we have

1+\dfrac{L]{d}≈1

So the Magnitude of the Electric Field at point P =
`(Q)/(4\pi \epsilon_0\ d^2)`