Question

point O lies in the interior of angle MNP. if the measure of MNO is x^2 + 10x, the measure of ONP is x^2 - 2x , and the measure of MNP is 3x^2 + 12, find the value of x. then find the measure of ONP

Answer 1

x = 6; ∠ONP = 24°

Explanation:

1. Find the value of x

`\begin{array}{rcl}\angle MNP & = & \angle MNO + \angle ONP\\3x^(2) + 12 & = & x^(2) + 10x + x^(2) - 2x\\3x^(2) + 12 & = & 2x^(2) + 8x\\x^(2) + 12 & = & 8x\\x^(2) -8x + 12 & = & 0\\(x - 2)(x - 6) & = & 0\\\end{array}`

`x = 2 \text{ or }x = 6`

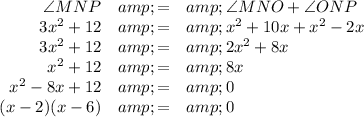
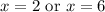
2. Find the measures of the angles

(a) x = 2

∠ ONP = x² - 2x = 2² - 2(2) = 4 - 4 = 0

This answer does not make sense because O lies in the interior of ∠MNP.

We disregard x = 2.

(b) x = 6

∠ ONP = x² - 2x = 6² - 2(6) = 36 - 12 = 24