Question

A body of mass m moves in a horizontal direction such that at time t its position is given byx(t)=at4+bt3+ct,where a, b, and c are constants. (a) What is the acceleration of the body? (b) What is the time-dependent force acting on the body?

Answer 1

The acceleration is given by de second derivative of x(t) which is equal to
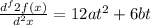`\frac{d^f{2}f(x) }{d^(2)x }=12at^(2) + 6bt` m/s^2

Step-by-step explanation:

a) We have the equation x(t)=at^4+bt^3+ct which is the position of the body of mass m at a time t

Where a, b and c are constants

From the rules of differenciation we have that the first derivative of the position is the velocity and the second derivative is the acceleration.

Hence the first derivative of the function is equal to
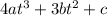`4at^(3) +3bt^(2)+c`[/tex] m/s

Don´t forget to write down the unities

Then we have to derivate again this equation, so we have

`[tex](d^(2)f(x) )/(d^(2)x )=12at^(2) + 6bt` m/s^2[/tex]

b) Remembering the Newton´s laws we know that

`F=ma`

where:

F is the force

m is the mass

and a is the acceleration

From the first part we know the value of the acceleration which is

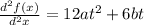`(d^(2)f(x) )/(d^(2)x )=12at^(2) + 6bt` m/s^2

So using the second law formula and replacing the values we have that

F=m(
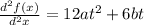`(d^(2)f(x) )/(d^(2)x )=12at^(2) + 6bt` ) N

Remember the that N= Newton which is kg*m/s^2