Question

An instructor gives her class the choice to do 7 questions out of the 10 on an exam.

(a)How many choices does each student have?
(b)How many choices does a student have if he/she must answer at least 3 of the first 5 questions?

Answer 1

(a) 120 choices

(b) 110 choices

Explanation:

The number of ways in which we can select k element from a group n elements is given by:

`nCk=(n!)/(k!(n-k)!)`

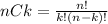
So, the number of ways in which a student can select the 7 questions from the 10 questions is calculated as:

`10C7=(10!)/(7!(10-7)!)=120`

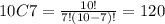
Then each student have 120 possible choices.

On the other hand, if a student must answer at least 3 of the first 5 questions, we have the following cases:

1. A student select 3 questions from the first 5 questions and 4 questions from the last 5 questions. It means that the number of choices is given by:

`(5C3)(5C4)=(5!)/(3!(5-3)!)*(5!)/(4!(5-4)!)=50`

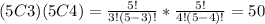
2. A student select 4 questions from the first 5 questions and 3 questions from the last 5 questions. It means that the number of choices is given by:

`(5C4)(5C3)=(5!)/(4!(5-4)!)*(5!)/(3!(5-3)!)=50`

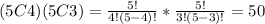
3. A student select 5 questions from the first 5 questions and 2 questions from the last 5 questions. It means that the number of choices is given by:

`(5C5)(5C2)=(5!)/(5!(5-5)!)*(5!)/(2!(5-2)!)=10`

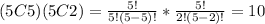
So, if a student must answer at least 3 of the first 5 questions, he/she have 110 choices. It is calculated as:

50 + 50 + 10 = 110