Question

A drunken sailor stumbles 580 meters north, 530 meters northeast, then 480 meters northwest. What is the total displacement and the angle of the displacement? (Assume east is the +x-direction and north is the +y-direction.)

a) What's the magnitude?
b) What's the direction? (In degrees and counterclockwise to the x-axis.)

Answer 1

(a) 1294.66 m

(b) 88.44°

Step-by-step explanation:

d1 = 580 m North

d2 = 530 m North east

d3 = 480 m North west

(a) Write the displacements in vector forms

`\overrightarrow{d_(1)}=580\widehat{j}`

`\overrightarrow{d_(2)}=530\left ( Cos45\widehat{i}+Sin45\widehat{j} \right )`

`\overrightarrow{d_(2)}=374.77\widehat{i}+374.77\widehat{j}`

`\overrightarrow{d_(3)}=480\left ( - Cos45\widehat{i}+Sin45\widehat{j} \right )`

`\overrightarrow{d_(3)}=-339.41\widehat{i}+339.41widehat{j}`

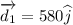
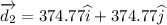
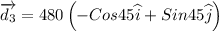
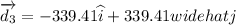
The resultant displacement is given by

`\overrightarrow{d}\overrightarrow{d_(1)}+\overrightarrow{d_(2)}+\overrightarrow{d_(3)}`

`\overrightarrow{d}=\left ( 374.77-339.41 \right )\widehat{i}+\left ( 580+374.77+339.41 \right )\widehat{j}`

`\overrightarrow{d}=35.36\widehat{i}+1294.18\widehat{j}`

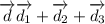
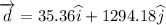
magnitude of the displacement

`d ={\sqrt{35.36^(2)+1294.18^(2)}}=1294.66 m`

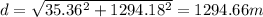
d = 1294.66 m

(b) Let θ be the angle from + X axis direction in counter clockwise

`tan\theta =(1294.18)/(35.36)=36.6`

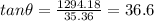
θ = 88.44°