Question

8. Charlene is looking into cell phone plans. Cell Plus gives unlimited minutes for $50/month. A1 Cell offers a $40 monthly fee, plus 5¢/min for any time over 300 min per month.

a) Write a linear equation to represent the charges for each company.
b) Graph the two equations to find the point of intersection.
c) What does the point of intersection represent?
d) Which plan should Charlene choose if she estimates that she will use her phone
10 h per month? 6 h per month?

Answer 1

See explanation

Explanation:

Let x be the number of minutes Charlene uses her phone per month and $y be the charge (in dollars) for x minutes of usage the phone.

A. Cell Plus gives unlimited minutes for $50/month. This paln doesn't depend on time, so

`y=50`

A1 Cell offers a $40 monthly fee, plus $0.05/min for any time over 300 min per month, then

`y=40+0.05(x-300)\\ \\y=40+0.05x-15\\ \\y=25+0.05x`

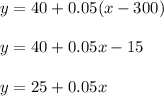
B. Attached diagram shows the graphs of these two functions.

C. The point of intersection is (500,50) and it represents the number of minutes x=500 when to plans have the same charges.

D. 10 hours = 600 minutes.

Cell plus charge = $50

A1 Cell charge
`=25+0.05\cdot 600=\$55`

Charlene has to choose Cell plus plan in this case.

6 hours = 360 minutes

Cell plus charge = $50

A1 Cell charge
`=25+0.05\cdot 360=\$43`

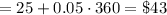
Charlene has to choose A1 Cell plan in this case.