Question

An athlete crosses a 25-m-wide river by swimming perpendicular to the water current at a speed of 0.5 m/s relative to the water. He reaches the opposite side at a distance 40 m downstream from his starting point.

1) How fast is the water in the river flowing with respect to the ground?
2) What is the speed of the swimmer with respect to a friend at rest on the ground?

Answer 1

The river current is flowing at a speed of 0.8 m/s concerning the ground, and the swimmer's speed concerning a friend on the ground is approximately 0.94 m/s.

Step-by-step explanation:

An athlete swims across a 25-m-wide river with a speed of 0.5 m/s perpendicular to the water current. The swimmer is carried 40 m downstream, indicating the presence of a river current. To find the speed of the river current, we use the Pythagorean theorem since the swimmer's motion relative to the river and the river's motion relative to the ground are perpendicular to each other.

The time taken to cross the river is the width of the river divided by the swimmer's speed concerning the water:
Time = 25 m / 0.5 m/s = 50 s. Now, the speed of the river current can be calculated using the downstream distance covered (40 m) and time (50 s): Speed of river = Distance downstream / Time = 40 m / 50 s = 0.8 m/s.

To calculate the swimmer's speed relative to the ground, we consider both the swimmer's speed across the river and the river's current speed. Using the Pythagorean theorem:
Swimmer's speed relative to the ground = √((0.5 m/s)^2 + (0.8 m/s)^2) = √(0.25 + 0.64) m/s = √(0.89) m/s ≈ 0.94 m/s.

Answer 2

1) Vx=0.8 m/s

2) V=0.94339 m/s

Step-by-step explanation:

We know that the speed to cross the river is 0.5 m/s. This is our y axis. Vy

And we don't know the speed of the river. This is in our x axis. Vx

Since we know that the shore is 25m away, and we have a 0.5m/s of speed.

We can find with y=v.t

Since we know y=25m and v=0.5m/s

We can find that 50 seconds is the time we take to cross the river.

Now we need to calculate the velocity of the river, for that we use the same equation, x=v.t where x is 40m at downstream, and t now we know is 50 seconds.

We can find that v of the river, or Vx is 0.8 m/s.

With the two components of the velocity we use this equation to calculate the module or the velocity of the swimmer respect a fix point on the ground.

`V=\sqrt{(Vx)^(2)+(Vy)^(2)  }`

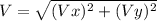
We replace the values of Vx and Vy and we find. V=0.94339 m/s.