Answer:
1) The absolute pressure equals = 96.98 kPa
2) Absolute pressure in terms of column of mercury equals 727 mmHg.
Step-by-step explanation:
using the equation of pressure statics we have
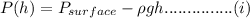
Now since it is given that at 6400 meters pressure equals 45 kPa absolute hence from equation 'i' we obtain
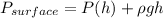
Applying values we get
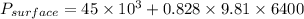

Now the pressure in terms of head of mercury is given by
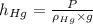
Applying values we get
