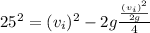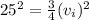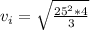Answer:

Step-by-step explanation:
Conceptual analysis
We apply the kinematic formula for an object that moves vertically upwards:
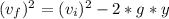
Where:
 : final speed in ft/s
: final speed in ft/s
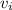 : initial speed in ft/s
: initial speed in ft/s
g: acceleration due to gravity in ft/s²
y: vertical position at any time in ft
Known data
For
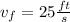 ,
,
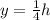 ; where h is the maximum height
; where h is the maximum height
for y=h,
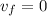
Problem development
We replace
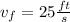 ,
,
 in the formula (1),
in the formula (1),
[
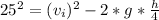 Equation (1)
Equation (1)
in maximum height(h):
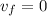 , Then we replace in formula (1):
, Then we replace in formula (1):
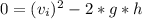
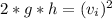
 Equation(2)
Equation(2)
We replace (h) of Equation(2) in the Equation (1) :