Question

Alice drops a rock down from a 40 meter tall building (vAlice,i = 0) at the same time that Bob (lying on the ground) throws a rock straight upwards from the ground with vBob,i = 20 m/s. At what height do the rocks pass each other?

Answer 1

Rocks will pass each other at 20.4m.

Step-by-step explanation:

Alice drops the rock from
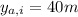`y_(a,i)=40m` (y is in the vertical axis) at
`v_(a,i)=0`.

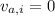Bob throws the rock from
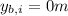`y_(b,i)=0m` at
`v_(b,i)}=20(m)/(s)`.

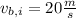`g` is gravity's acceleration.

Position equation for alice's rock:

`y_(a)(t)=y_(a,i) +v_(a,i)t - (1)/(2)gt^(2) =40m-(1)/(2)gt^(2)`

Position equation for Bob's rock:

`y_(b)(t)=y_(b,i) + v_(b,i)t - (1)/(2)gt^(2) =20(m)/(s)t -(1)/(2)gt^(2)`

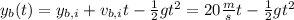
We we'll first find the time
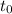`t_(0)` at which the rocks meet. For this, we will equalize Bob's and Alice's equations:

`y_(a)(t_(0))=y_(b)(t_(0))`

`40m-(1)/(2)gt_(0)^(2)=20(m)/(s)t_(0) -(1)/(2)gt_(0)^(2)`

⇒
`20(m)/(s)t_(0)=40m` ⇒
`t_(0)=2s`

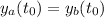
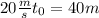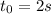
So, we can take
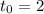`t_(0)=2` and just put it in any of the two laws of motion to see at what height the rocks meet. We will take Alice's equation (using g=9.8m/s):

`y_(a)(2) =40m-(1)/(2)g2^(2)=20.4m`

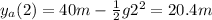
Rocks will pass each other at 20.4m.