Question

Earth's oceans have an average depth of 3800 m, a total area of 3.63 × 108 km2, and an average concentration of dissolved gold of 5.8 × 10−9 g/L. How many grams of gold are in the oceans?

Answer 1

8.00 *10¹² g

Explanation:

We must calculate the grams of gold in the ocean.

We are given the concentration of dissolved gold as grams per Liter.

So we need to first calculate the Liters of the ocean, that is, the volume.

We can calculate the volume of the ocean assuming a prism shape as:

Volume = Area x Depth

• Depth = 3800 m
• Area = 3.63 x10⁸ km²

We should first convert the area from km² to m² so that the units are consistent:

`3.63 *10^(8)  km^(2) * ((1000 m)/(1 km) )^(2) = 3.63 *10^(14)  m^(2)`

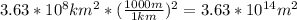
So the volume:

Volume = 3.63 x10¹⁴ m² * 3800 m = 1.38 x10¹⁸ m³

Since we have the concentration given in Liters, lets convert the volume to Liters, knowing that 1 L = 1000 m³:

`1.38 *10^(18) m^(3) *(1000 L)/(1 m^(3) ) = 1.38 *10^(21) L`

Knowing that the concentration of gold is 5.8 *10⁻⁹ grams per Liter, we can multiply this value by the Liters of the ocean to calculate the grams of gold:

5.8 *10⁻⁹ g/L x 1.38 *10²¹ L = 8.00 *10¹² g

There are 8.00 *10¹² grams of gold in the ocean

Answer 2

grams of gold=8x10^12 g

Explanation:

first we calculate the volume of the ocean this is achieved by multiplying the area by the depth

A=3.63x10^8 km^2=3.63x10^14 m^2

V=AxL

V=3.63x10^14 x 3800=1.3797x10^18m^3=1.3797x10^21L

then we multiply the volume in liters by the concentration of gold in the ocean per liter

grams of gold=1.3797x10^21 x 5.8x10^-9=8x10^12 g