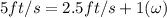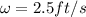Answer:
Part a)
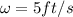 counterclockwise
counterclockwise
Part b)
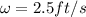 counterclockwise
counterclockwise
Part c)
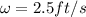 clockwise
clockwise
Step-by-step explanation:
Let the cart has radius R = 1 ft
so here we have speed of the center of the cart is
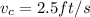
let the angular speed is given as
 counter clockwise
counter clockwise
Part a)
if the top most point of the rim has same speed as that of speed of the center but it is towards left
so we have

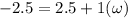
so we have
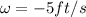
Part b)
if the speed of the top point on the rim is zero

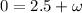
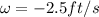
Part c)
if the speed at the top position on the rim is 5 ft/s