Answer:
90 mi/h
Explanation:
Given,
For first 30 miles, her speed is 30 miles per hour,
Let x be her speed in miles per hour for another 30 miles,
Since, here the distance are equal in each interval,
So, the average speed of the entire journey
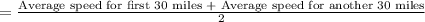
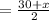
According to the question,


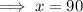
Hence, she needs to go 90 miles per hour for remaining 30 miles.