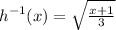Question

4TH TIME ASKING THIS!!! Please help me! Someone pleaseeee. I need the correct answers. I don’t want to fail

Answer 1

The functions are inverses; f(g(x)) = x ⇒ answer D

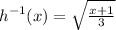`h^(-1)(x)=\sqrt{(x+1)/(3)}` ⇒ answer D

Explanation:

* Lets explain how to find the inverse of a function

- Let f(x) = y

- Exchange x and y

- Solve to find the new y

- The new y =
`f^(-1)(x)`

* Lets use these steps to solve the problems

∵
`f(x)=√(x-3)`

∵ f(x) = y

∴
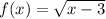
`y=√(x-3)`

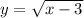
- Exchange x and y

∴
`x=√(y-3)`

- Square the two sides

∴ x² = y - 3

- Add 3 to both sides

∴ x² + 3 = y

- Change y by
`f^(-1)(x)`

∴
`f^(-1)(x)=x^(2)+3`

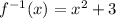
∵ g(x) = x² + 3

∴
`f^(-1)(x)=g(x)`

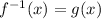
∴ The functions are inverses to each other

* Now lets find f(g(x))

- To find f(g(x)) substitute x in f(x) by g(x)

∵
`f(x)=√(x-3)`

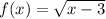
∵ g(x) = x² + 3

∴
`f(g(x))=\sqrt{(x^(2)+3)-3}=\sqrt{x^(2)+3-3}=\sqrt{x^(2)}=x`

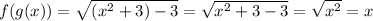
∴ f(g(x)) = x

∴ The functions are inverses; f(g(x)) = x

* Lets find the inverse of h(x)

∵ h(x) = 3x² - 1 where x ≥ 0

- Let h(x) = y

∴ y = 3x² - 1

- Exchange x and y

∴ x = 3y² - 1

- Add 1 to both sides

∴ x + 1 = 3y²

- Divide both sides by 3

∴
`(x + 1)/(3)=y^(2)`

- Take √ for both sides

∴ ±
`\sqrt{(x+1)/(3)}=y`

∵ x ≥ 0

∴ We will chose the positive value of the square root

∴
`\sqrt{(x+1)/(3)}=y`

- replace y by
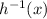
`h^(-1)(x)`

∴
`h^(-1)(x)=\sqrt{(x+1)/(3)}`