Answer:
Explanation:
Given that at a certain school, twenty-five percent of the students wear a watch and thirty percent wear a bracelet.
A- people who wear watch = 25%
B - people who wear bracelet = 30%
(AUB)' - People who wear neither a watch nor a bracelet=60%
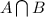 - People who wear both =100%-60% = 40%
- People who wear both =100%-60% = 40%
a)
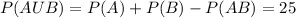
b) the probability that this student is wearing both a watch and a bracelet
=
