Question

Which inequality is represented by the graph?

A) y≥−12x+2.5

B) y>−2x+2.5

C) y≥−2x+2.5

D) y≤−2x+2.5

Answer 1

Answer: The answers C

Step-by-step explanation: Use Desmos to find it

Answer 2

Option C.

Explanation:

If a line passes through two points
`(x_1,y_1)` and
`(x_2,y_2)`, then the equation of line is

`y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)`

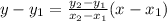
From the given graph it is clear that the related line passes thorough the points (0,2.5) and (2,-1.5).

The equation of related line is

`y-2.5=(-1.5-2.5)/(2-0)(x-0)`

`y-2.5=(-4)/(2)(x)`

`y-2.5=-2x`

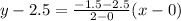
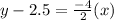
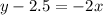
Add 2.5 on both sides.

`y-2.5+2.5=-2x+2.5`

`y=-2x+2.5`

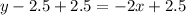
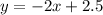
Th sign of inequality is either ≤ or ≥ because the related line is a solid line. It means the points on the line are included in the solution set.

Let the required inequality is

`y\geq -2x+2.5`

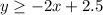
(1,1) is included in the shaded region. So, the above inequality is true for (1,1).

`1\geq -2(1)+2.5`

`1\geq 0.5`

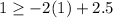
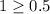
The assumed inequality is true for (1,1). So, the required inequality isn
`y\geq -2x+2.5`.

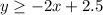Therefore, the correct option is C.