Question

Two train whistles have identical frequencies of 175 Hz. When one train is at rest in the station and the other is moving nearby, a commuter standing on the station platform hears beats with a frequency of 4.05 beats/s when the whistles operate together. What are the two possible speeds and directions the moving train can have? slower speed m/s Correct: Your answer is correct. faster speed m/s Changed: Your submitted answer was incorrect. Your current answer has not been submitted.

Answer 1

The speed of the train is 7.75 m/s towards station.

The speed of the train is 8.12 m/s away from the station.

Step-by-step explanation:

Given that,

Frequency of the whistles f= 175 Hz

Beat frequency
`\Delta f= 4.05 Hz`

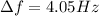
Speed of observer = 0

We need to calculate the frequency

Using formula of beat frequency

`\Delta f=f'-f`

`f'=\Delta f+f`

`f'=4.05+175`

`f'=179.05\ Hz`

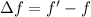
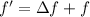
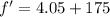
When the train moving towards station, then the frequency heard is more than the actual

Using Doppler effect

`f'=f((v-v_(o))/(v-v_(s)))`

`v=v-(vf)/(f')`

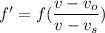
Put the value into the formula

`v=343-(343*175)/(179.05)`

`v=7.75\ m/s`

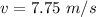
The speed of the train is 7.75 m/s towards station.

When the train moving away form the station

Again beat frequency

`\Delta f=f-f'`

`f'=f-\Delta`

`f'=175-4.05`

`f'=170.95\ Hz`

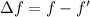
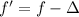
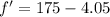
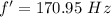
We need to calculate the speed

Using Doppler effect

`f'=f((v-v_(o))/(v+v_(s)))`

`v=(vf)/(f')-v`

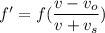
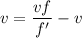
Put the value into the formula

`v=(343*175)/(170.95)-343`

`v=8.12\ m/s`

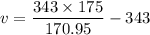
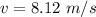
The speed of the train is 8.12 m/s away from the station.

Hence, This is the required solution.