Answer:
The time at which the pass each other on the road is 4:00 pm
Explanation:
The first step is to write the equations that give us the position of Emily and Anthony, these are give by:
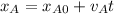for Anthony
for Emily
Since Antony drives 160 miles to Albany, we can claim that the distance from Kingstown to Albany is 160 miles.
Let us set the initial position of Antony in Kingstown and consider it as the origin of our coordinate system. In this way,
.
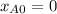This automatically tells us that Emily initial position, in Albany, is 160 miles from our origin, hence
.
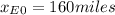Now, we need to define where to start counting the time. In this problem, it is easier to set time zero when Emily leaves. The reason for this is that now, we can say that when Emily left, Anthony was already traveling during 15 mins (remember Emily departing time was 2:15 pm and Anthony's time was 2:00 pm) and Anthony's initial position was from Emily's point of view was different from zero. We can calculate this distance as the multiplication of the time Anthony was traveling times the speed at which he was driving. This is:
being
the 15 mins he traveled before Emily started and
the 45 m.p.h given by the problem. We also need to convert 15 mins to hours, which gives 0.25 hours. Thus:
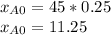miles
and the position equations are now:
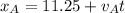for Anthony
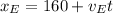
Since we are asked the time at which the pass each other on the road we need to equals their positions,
:
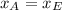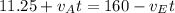
Notice here that Emily's position is negative since she is moving towards the origin of our system, meaning in the negative direction. Solving for
:
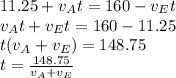
Substituting the values of
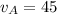and
:
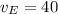What we have calculated is the time interval from where we start counting the time and remember this was set at 2:15 pm when Emily left. Since the exercise asks for the hours of the day we need to add the time interval to 2:15 pm and:
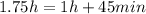
And 2:15 pm + 1 h is 3:15 pm + 45 mins is 4:00 pm which is the time at which the pass each other on the road.