Question

Please help with this limit i don’t know what to do at all!

Answer 1

We're given

`\displaystyle\lim_(x\to2)\sqrt{(f(x)^2-8x+3)/(x+1)}=9`

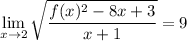
The function
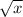`\sqrt x` is continuous for all
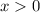`x>0`. If a function
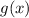`g(x)` is continuous, then

`\displaystyle\lim_(x\to c)g(h(x))=g\left(\lim_(x\to c)h(x)\right)`

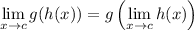
This allows us to pass the limit through the square root:

`\displaystyle\sqrt{\lim_(x\to2)(f(x)^2-8x+3)/(x+1)}`

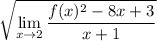
The limit of a quotient is the quotient of limits (provided the limit of the denominator is not 0):

`\sqrt{(\lim\limits_(x\to2)(f(x)^2-8x+3))/(\lim\limits_(x\to2)(x+1))}`

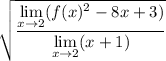
In the numerator, we can distribute the limit as

`\displaystyle\lim_(x\to2)(f(x)^2-8x+3)=\left(\lim_(x\to2)f(x)\right)^2+\lim_(x\to2)(3-8x)`

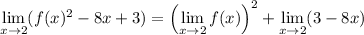
So we end up with

`\sqrt{(\left(\lim\limits_(x\to2)f(x)\right)^2+\lim\limits_(x\to2)(3-8x))/(\lim\limits_(x\to2)(x+1))}=\sqrt{\frac{\left(\lim\limits_(x\to2)f(x)\right)^2-13}3}=9`

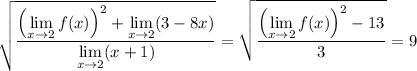
Then we just solve for the desired limit:

`\frac{\left(\lim\limits_(x\to2)f(x)\right)^2-13}3=81`

`\left(\lim\limits_(x\to2)f(x)\right)^2-13=243`

`\left(\lim\limits_(x\to2)f(x)\right)^2=256`

`\implies\lim\limits_(x\to2)f(x)=\pm16`

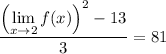
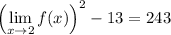
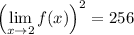
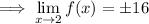
Obviously the limit can't have two values, so one of these is not right, but only the positive value is one of the answer choices, so the limit is 16.