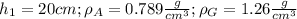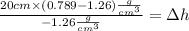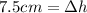Question

Glycerin is poured into an open U-shaped tube until the height in both sides is 20cm. Ethyl alcohol is then poured into one arm until the height of the alcohol column is 20cm. The two liquids do not mix. What is the difference in height between the top surface of the glycerin and the top surface of the alcohol?

Answer 1

7.5 cm

Step-by-step explanation:

In the figure we can see a sketch of the problem. We know that at the bottom of the U-shaped tube the pressure is equal in both branches. Defining
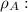`\rho_A:` Ethyl alcohol density and
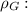`\rho_G:` Glycerin density , we can write:

`\rho_A* g * h_1 + \rho_G * g * h_2 = \rho_G * g * h_3`

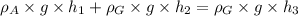
Simplifying:

`\rho_A* h_1 = \rho_G * (h_3 - h_2) (1)`

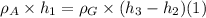
On the other hand:

`h_1 + h_2 = \Delta h + h_3`

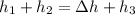
Rearranging:

`h_1 - \Delta h = h_3 - h_2 (2)`

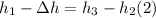
Replacing (2) in (1):

`\rho_A* h_1 = \rho_G * (h_1 - \Delta h)`

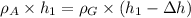
Rearranging:

`(h_1 * (\rho_A - \rho_G))/(- \rho_G) = \Delta h`

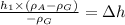
Data:

`h_1 = 20 cm; \rho_A = 0.789 (g)/(cm^3); \rho_G = 1.26 (g)/(cm^3)`

`(20 cm * (0.789 - 1.26) (g)/(cm^3))/(- 1.26(g)/(cm^3))  = \Delta h`

`7.5 cm =  \Delta h`