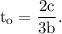Answer:
(a):
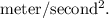
(b):
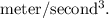
(c):
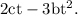
(d):
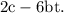
(e):
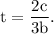
Step-by-step explanation:
Given, the position of the particle along the x axis is
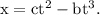
The units of terms
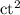 and
and
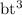 should also be same as that of x, i.e., meters.
should also be same as that of x, i.e., meters.
The unit of t is seconds.
(a):
Unit of
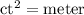
Therefore, unit of
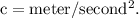
(b):
Unit of
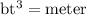
Therefore, unit of
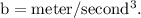
(c):
The velocity v and the position x of a particle are related as

(d):
The acceleration a and the velocity v of the particle is related as
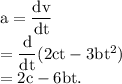
(e):
The particle attains maximum x at, let's say,
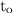 , when the following two conditions are fulfilled:
, when the following two conditions are fulfilled:
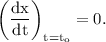
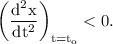
Applying both these conditions,
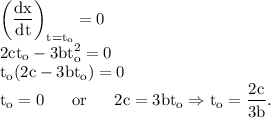
For
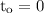 ,
,

Since, c is a positive constant therefore, for
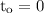 ,
,
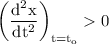
Thus, particle does not reach its maximum value at
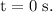
For
 ,
,

Here,
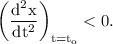
Thus, the particle reach its maximum x value at time