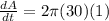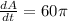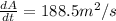Question

Suppose oil spills from a ruptured tanker and spreads in a circular pattern. If the radius of the oil spill increases at a constant rate of 1 m/s, how fast is the area of the spill increasing when the radius is 30 m?

Answer 1

`(dA)/(dt) = 188.5 m^2/s`

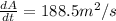
Step-by-step explanation:

As we know that area of the circle at any instant of time is given as

`A = \pi r^2`

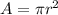
now in order to find the rate of change in area we will have

`(dA)/(dt) = 2\pi r(dr)/(dt)`

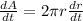
here we know that

rate of change of radius is given as

`(dr)/(dt)= 1 m/s`

radius of the circle is given as

`r = 30 m`

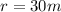
now we have

`(dA)/(dt) = 2\pi (30)(1)`

`(dA)/(dt) = 60\pi`

`(dA)/(dt) = 188.5 m^2/s`