Answer:
The particle in the D ring is 1399 times faster than the particle in the Encke Division.
Step-by-step explanation:
The circular velocity is define as:
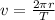
Where r is the radius of the trajectory and T is the orbital period
To determine the circular velocity of both particles it is necessary to know the orbital period of each one. That can be done by means of the Kepler’s third law:

Where T is orbital period and r is the radius of the trajectory.
Case for the particle in the Encke Division:


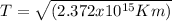
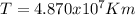
It is necessary to pass from kilometers to astronomical unit (AU), where 1 AU is equivalent to 150.000.000 Km (
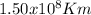 )
)
1 AU is defined as the distance between the earth and the sun.
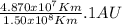
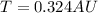
But 1 year is equivalent to 1 AU according with Kepler’s third law, since 1 year is the orbital period of the earth.
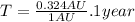
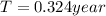
That can be expressed in units of days
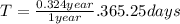
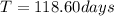
Circular velocity for the particle in the Encke Division:
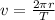
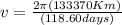
For a better representation of the velocity, kilometers and days are changed to meters and seconds respectively.
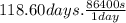 ⇒ 10247040 s
⇒ 10247040 s
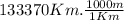 ⇒ 133370000 m
⇒ 133370000 m
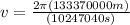
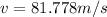
Case for the particle in the D Ring:
For the case of the particle in the D Ring, the same approach used above can be followed


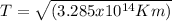




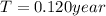
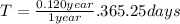
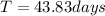
Circular velocity for the particle in D Ring:
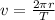
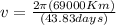
For a better representation of the velocity, kilometers and days are changed to meters and seconds respectively.
 ⇒ 3786912 s
⇒ 3786912 s
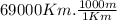 ⇒ 69000000 m
⇒ 69000000 m
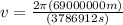
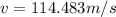

The particle in the D ring is 1399 times faster than the particle in the Encke Division.