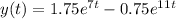Question

The solution of a certain differential equation is of the form y(t)=aexp(7t)+bexp(11t), where a and b are constants. The solution has initial conditions y(0)=1 and y′(0)=4. Find the solution by using the initial conditions to get linear equations for a and b.

Answer 1

y(t) = a exp(3t) + b exp(4t) conditions, y(0) = 3 y'(0) = 3 y(0) = a exp(3 x 0) + b exp(4 x 0) = a exp(0) + b exp(0) = (a x 1) + (b x 1) = a + b y'(0) = 0 so the linear equation is, a + b = 3

Explanation:

Answer 2

Explanation:

Given that the solution of a certain differential equation is of the form

`y(t) = ae^(7t) +be^(11t)`

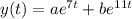
Use the initial conditions

i) y(0) =1

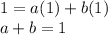`1=a(1)+b(1)\\a+b=1` ... I

ii) y'(0) = 4

Find derivative of y first and then substitute

`y'(t) = 7ae^(7t) +11be^(11t)\\y'(0) =7a+11b \\7a+11b =4 ...II`

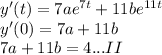
Now using I and II we solve for a and b

Substitute b = 1-a in II

`7a+11(1-a) = 4\\-4a+11 =4\\-4a =-7\\a = 1.75 \\b = -0.75`

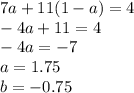
Hence solution is

`y(t) = 1.75e^(7t) -0.75e^(11t)`