Question

Find each of the following functions. f(x) = 3 − x , g(x) = x2 − 4 (a) f + g State the domain of the function. (Enter your answer using interval notation.) (b) f − g State the domain of the function. (Enter your answer using interval notation.) (c) fg State the domain of the function. (Enter your answer using interval notation.) (d) f/g State the domain of the function. (Enter your answer using interval notation.)

Answer 1

Answer with Step-by-step explanation:

We are given that
`f(x)=3x-2,g(x)=x^2-4`

We have to find the

a.Domain of f+g

Domain of f(x)=(
`-\infty,\infty`)

Suppose y=g(x)=
`x^2-4`

`x=√(y+4)`

Therefore,
`g^(-1)(x)=√(x+4)`

Domain of
`g^(-1)(x)=[-4,\infty)`

Range of
`g^(-1)(x)=[0,\infty)`

Range of
`g^(-1)(x)`=Domain of g(x)=
`[0,\infty)`

Domain of (f+g)(x)=[0,
`\infty`)

Because domain of sum of two function is the intersection of domain of given functions.

Similar, domain of (f-g)(x)=[0,
`\infty`)

Because domain of difference of two function is the intersection of domain of given functions.

Similarly , domain of fg(x)=[0,
`\infty`)

Because domain of product of two function is the intersection of domain of given functions.

`(f)/(g)(x)=(3-x)/(x^2-4)=(3-x)/((x-2)(x+2))`

Function is not define at x=2 and x=-2

Therefore, domain of
`(f)/(g)(x)`=R-{-2,2}=
`(-\infty,-2)\cup(-2,2)\cup(2,\infty)`

Answer 2

(a)
`(f+g)(x)=x^2-x-1`; Domain = (-∞,∞)

(b)
`(f-g)(x)=-x^2-x+7`; Domain = (-∞,∞)

(c)
`(fg)(x)=-x^3+3x^2+4x-12`; Domain = (-∞,∞)

(d)
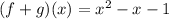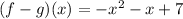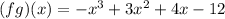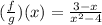`((f)/(g))(x)=(3-x)/(x^2-4)`; Domain = (-∞,-2)∪(-2,2)∪(2,∞)

Explanation:

The given functions are

`f(x)=3-x`

`g(x)=x^2-4`

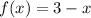
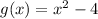
(a)

We need to find the function f+g.

`(f+g)(x)=f(x)+g(x)`

`(f+g)(x)=(3-x)+(x^2-4)`

`(f+g)(x)=x^2-x-1`

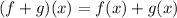
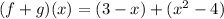
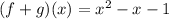
It is a polynomial and domain of a polynomial is all real numbers.

Domain = (-∞,∞)

(b)

We need to find the function f-g.

`(f-g)(x)=f(x)-g(x)`

`(f-g)(x)=(3-x)-(x^2-4)`

`(f-g)(x)=3-x-x^2+4`

`(f-g)(x)=-x^2-x+7`

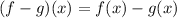
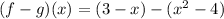
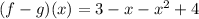
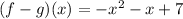
It is a polynomial. So,

Domain = (-∞,∞)

(c)

We need to find the function fg.

`(fg)(x)=f(x)g(x)`

`(fg)(x)=(3-x)(x^2-4)`

`(fg)(x)=3(x^2-4)-x(x^2-4)`

`(fg)(x)=3x^2-12-x^3+4x`

`(fg)(x)=-x^3+3x^2+4x-12`

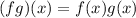
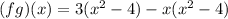
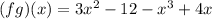
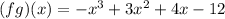
It is a polynomial. So,

Domain = (-∞,∞)

(d)

We need to find the function f/g.

`((f)/(g))(x)=(f(x))/(g(x))`

`((f)/(g))(x)=(3-x)/(x^2-4)`

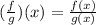
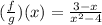
It is a rational function. Domain of a rational function is all real except those values at which the denominator is equal to 0.

Equate denominator equal to 0.

`x^2-4=0`

`x^2=4`

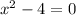
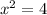
Taking square both sides.

`x=\pm √(4)`

`x=\pm 2`

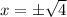
The function is not defined for x=-2 and x=2. So, domain of f/g is all real numbers except -2 and 2.

Domain = (-∞,-2)∪(-2,2)∪(2,∞)