Answer: 0.2643
Explanation:
Given : The proportion of adults are unemployed : p=0.077
The sample size = 300
By suing normal approximation to the binomial , we have

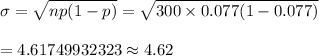
Now, using formula
 , the z-value corresponding to 26 will be :-
, the z-value corresponding to 26 will be :-
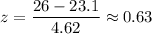
Using standard distribution table for z , we have
P-value=

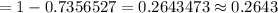
Hence, the probability that at least 26 in the sample are unemployed =0.2643