Question

A real estate agent has surveyed houses in several nearby zip codes in an attempt to put together a comparison for a new property that she would like to put on the market. The 583 houses she surveyed have a mean price of $176,678 with a standard deviation of $61,029. The mean house size is 1,676 square ft, with a standard deviation of 582 square ft. (Use 2 decimal places for the questions below.) Which is more unusual in this market: a house in that sells for $357,000 or a house with an area of 3,600 square ft?

Answer 1

The house with an area 3,600 square feet is more unusual

Explanation:

Given:

Number of houses surveyed = 583

Mean price = $176,678

Standard deviation = $61,029

Mean house size = 1,676 square ft

standard deviation = 582 square ft

Now,

the as z score =
`\frac{\textup{(X - mean )}}{\textup{standard deviation}}`

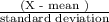
thus,

for selling value of $357,000

z score =
`\frac{\textup{(357,000 - 176,678 )}}{\textup{61,029}}`

or

z score = 2.95

and for house with an area 3,600 square feet

z score =
`\frac{\textup{(3600 - 1676)}}{\textup{582}}`

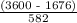
or

z score = 3.30

Hence, the house with an area 3,600 square feet is more unusual