Answer:
The average rate of change of the population on the intervals [ 5 , 10 ] , [ 5 , 9 ] , [ 5 , 8 ] , [ 5 , 7 ] , and [ 5 , 6 ] are 734.504, 733.06, 731.62, 730.185 and 728.75 respectively.
Explanation:
The given function is
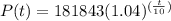
where, P(t) is population after t years.
At t=5,
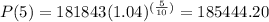
At t=6,
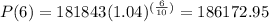
At t=7,

At t=8,
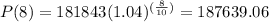
At t=9,
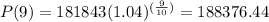
At t=10,
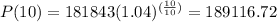
The rate of change of P(t) on the interval
![[x_1,x_2]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/s2dz1kqfrnthao9ifgtcsxy77c95z697oo.png) is
is
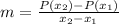
Using the above formula, the average rate of change of the population on the intervals [ 5 , 10 ] is
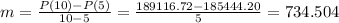
The average rate of change of the population on the intervals [ 5 , 9 ] is
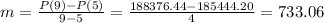
The average rate of change of the population on the intervals [ 5 , 8 ] is
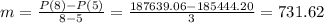
The average rate of change of the population on the intervals [ 5 , 7 ] is
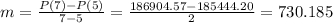
The average rate of change of the population on the intervals [ 5 , 6 ] is
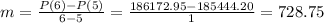
Therefore the average rate of change of the population on the intervals [ 5 , 10 ] , [ 5 , 9 ] , [ 5 , 8 ] , [ 5 , 7 ] , and [ 5 , 6 ] are 734.504, 733.06, 731.62, 730.185 and 728.75 respectively.