Question

Find each of the following for ​f(x) = 3x^2 - 5x + 7. ​

(A) f(x + h) ​
(B) f(x + h) - f(x) ​
(C) [f(x + h) - f(x)]/h

Answer 1

Answer: The evaluations are done below.

Step-by-step explanation: We are given the following function :

`f(x)=3x^2-5x+7.`

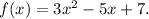
We are to find the value of the following expressions :

`(A)~f(x+h)\\\\(B)~f(x+h)-f(x)\\\\(C)~(f(x+h)-f(x))/(h)`

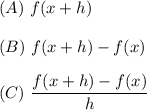
To find the above expressions, we must use the given value of f(x) as follows :

`(A)~\textup{We have}\\\\f(x+h)\\\\=3(x+h)^2-5(x+h)+7\\\\=3(x^2+2xh+h^2)-5x-5h+7\\\\=3x^2+6xh+3h^2-5x-5h+7.`

`(B)~\textup{We have}\\\\f(x+h)-f(x)\\\\=(3x^2+6xh+3h^2-5x-5h+7)-(3x^2-5x+7)\\\\=6xh+3h^2-5h.`

`(C)~\textup{We have}\\\\(f(x+h)-f(x))/(h)\\\\\\=(6xh+3h^2-5h)/(h)\\\\\\=(h(6x+3h-5))/(h)\\\\=6x+3h-5.`

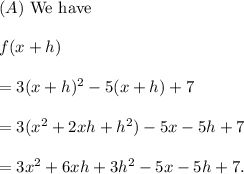
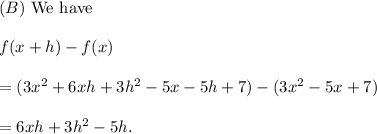
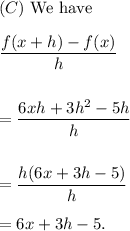
Thus, all the expressions are evaluated.